티스토리 뷰
유한요소법(FINITE ELEMENT METHOD)을 이용한 CAE과정에서 주어진 문제에 적합한 해석 소프트웨어 혹은 접근 방법의 두가지 선택 사항이 바로 EXPLICIT으로 해석할것이냐 IMPLICIT으로 해석할 것이냐이다. 둘다 접근 가능한 문제도 심심치 않게 있다.
implicit finite element method는 내연적 유한요소법,
explicit finite element method는 외연적 유한요소법이라고 한다. 둘의 차이점을 살펴보면 다음과 같다.
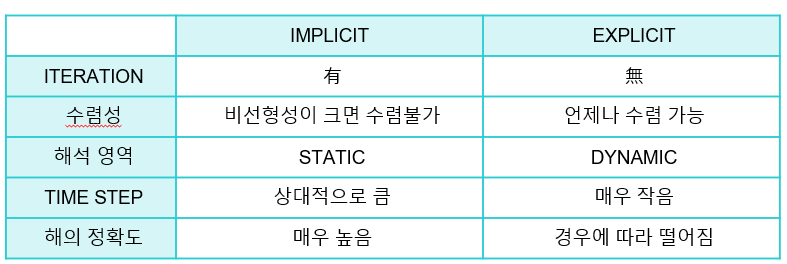
내연적 유한요소법의 가장 큰 특징은 반복계산에 있다(iteration). 이 과정은 구조해석 문제에서 풀게 되는 3가지 방정식 평형 방정식, 구성 방정식, 적합 방적식을 연립하여 해를 구하는 프로세스이다. 적당한 TIME STEP(시간증분) 이 주어지면 그 시점에서의 평형, 구성, 적합 방정식을 만족하는 해를 구해 나가게 된다. 이 답을 구하기 위해 여러번 반복 계산을 하게 된다.
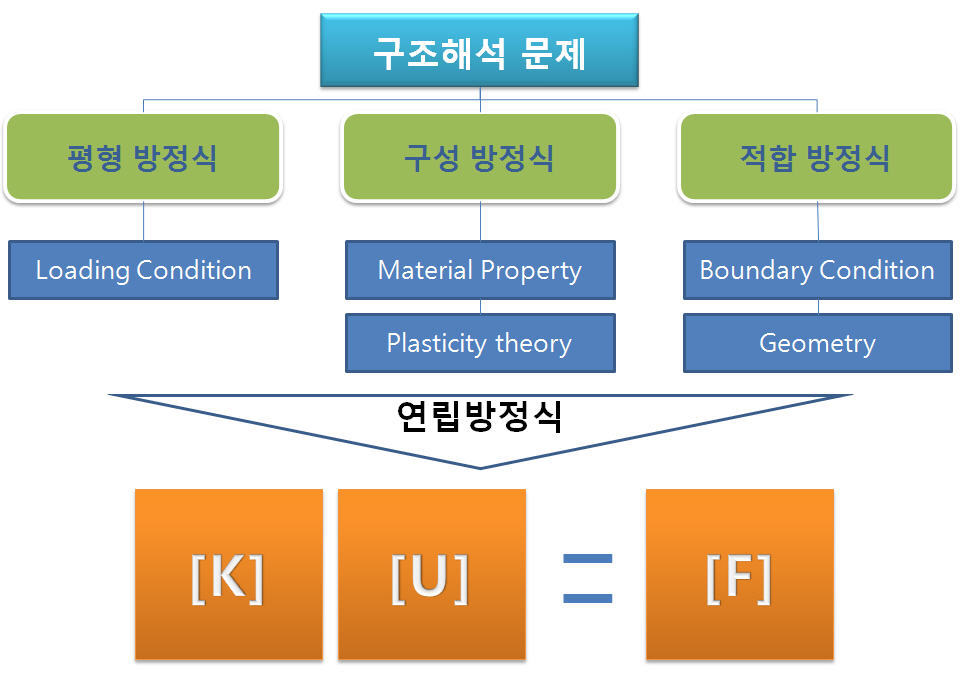
결국 반복 계산에서 풀게 되는 것은 연립방정식을 하나의 큰 매트릭스 형태로 만든 강성행렬입니다. 위의 그림에서 보여주는 [K]라는 행렬이 그에 해당하겠습니다. 이것은 요소의 수, 접촉 조건, 경계 조건, 하중 조건, 등에 의해 그 크기가 결정되며 크기가 커질수록 가우스 소거법등의 알고리즘을 적용하는 것이 만만치 않아집니다.
때에 따라서는 수렴이 결국 되지 않고 계산 불능의 상태가 되기도 합니다. 이것이 IMPLICIT의 최대 단점이라고 할수 있습니다. 그러나 수렴만 되면 그 해는 모든 방정식을 다 고려해서 EXACT SOLUTION을 찾아 낸 것이기 때문에 높은 정확도를 갖게 됩니다.
스프링백 해석이나 좌굴 해석 같이 정확도가 매우 높게 요구되는 경우에는 IMPLICIT을 주로 사용하는 것이 적합하다고 생각합니다.
그러나 비선형성이 높은 문제에서는 IMPLICIT은 결국 답을 못얻어 낼수 있는 위험이 있습니다. 비선형성이라 하면 크게 3가지로 말할수 있습니다.
1. 재료의 비선형성: 소성영역까지 고려할 때는 필수적입니다. 거의 모든 재료는 사실상 비선형성입니다.
2. 접촉의 비선형성: 접촉은 모든 해석에서 어려움을 주는 난제가 아닐수 없습니다.
3. 형상의 비선형성: 형상이 비대칭적이고 비선형적인 경우, 요즘의 대부분의 제품이 유선형의 비대칭적 바디인경우가 많습니다.
비선형성이 강한 문제일수록 결국 EXPLICIT으로 접근을 해야합니다. EXPLICIT은 강성행렬을 풀어나가는 것이 아니고 이전 단계의 값을 다음단계에 대입함으로 해를 얻어 갑니다. 따라서 수렴에대한 부담이 없습니다. 해는 반드시 구해지게 됩니다. 그러나 그 정확도가 문제 겠죠.
EXPLICIT의 경우 해의 정확도를 높이기 위해서는 TIME STEP을 매우 작게 하는 방법을 써야 합니다. 일반적으로 비선형성이 클수록 TIME STEP은 더 작아져야 합니다.
그러나 또 문제는 해석 시간입니다. TIME STEP을 무한정 작게 잡을 수 없는 이유는 기하급수적으로 늘어나는 해석 시간 때문입니다. 최적의 TIME STEP은 몇이냐? 이것은 그때 그때 달라요. 따라서 엔지니어의 판단에 달려 있습니다.
아무리 좋은 툴이라 해도 엔지니어에게 문제 해결의 실마리는 달려 있습니다.
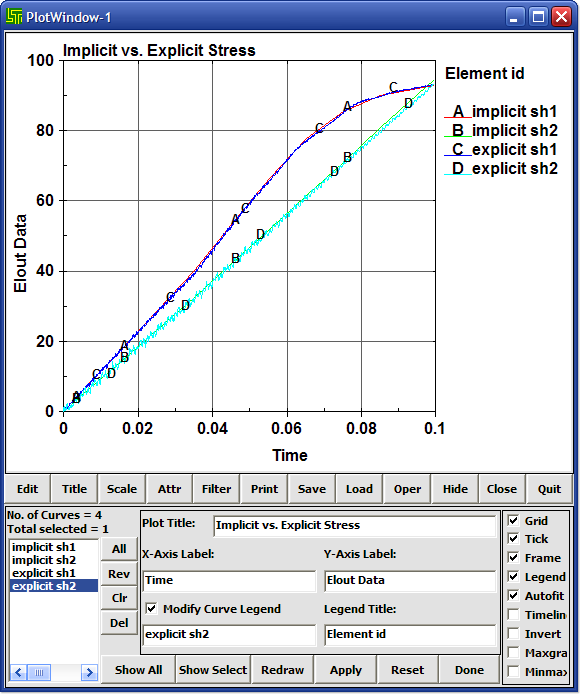
위의 그림에서 볼수 있듯이 EXPLICIT의 경우에는 결과 값의 FLUCTUATION이 있지만 잘 FILTERING한다면 IMPLICIT으로 풀었을 경우와 차이 없는 해를 구할수 있게 됩니다. 어떤 방법으로 접근하느냐도 결국 엔지니어의 선택에 달려 있습니다.
'STORY > 시뮬레이션' 카테고리의 다른 글
| CAE 도입 실패의 이유 (4) | 2021.05.01 |
|---|---|
| 적절한 시뮬레이션 시간은? (0) | 2020.12.14 |
| MESH FREE CAE 소프트웨어 DAFUL (0) | 2014.04.11 |
| [ANSYS] 전기-열전달 연성해석 (3) | 2014.03.13 |
| LS-DYNA에서 제공되는 HISTORY VARIAVLES (2) | 2012.09.06 |
- Total
- Today
- Yesterday
- 올란도
- 유한요소해석
- 시뮬레이션
- MIND
- 구조해석
- 배드민턴 스매싱
- mental
- NFX
- ok저축은행
- life mechanics
- 강원도여행
- 유한요소법
- 샤오미
- 맛집
- CAE 소프트웨어
- 배드민턴 리시브
- 다이어트
- 배드민턴 수비
- 플랭크
- FEM
- 카페
- 물회
- stress
- 접촉알고리즘
- 마이다스아이티
- 미세먼지
- CAE
- 상급자 라켓
- ls-dyna
- 쉐보레
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
